Armstrong Sayı: Tanımı, Özellikleri ve Bulma Yöntemleri

Giriş Matematikte birçok ilginç sayı kavramı bulunmaktadır. Bu makalede, Armstrong sayılarından bahsedeceğiz. Armstrong sayıları, sayıların rakamlarının küplerinin toplamının kendisine eşit olduğu sayılardır. Örneğin, 153 bir Armstrong sayısıdır çünkü 1^3 + 5^3 + 3^3 = 153’e eşittir.

Tarihçe Armstrong sayıları, ismini Amerikalı matematikçi Michael F. Armstrong’dan almıştır. Armstrong, 1969 yılında bir matematik yarışmasında bu tür sayıları tanımlamıştır. Ancak, bu sayılar aslında öncesinden bilinmektedir ve Hindu-Arap rakamlarının kullanımı ile ilgili eski bir fenomendir. Armstrong, bu tür sayıları popüler hale getiren kişi olmuştur.

Kullanım Alanları Armstrong sayıları, matematiksel teorilerde ve programlama dillerinde kullanışlı olabilir. Aşağıda bazı kullanım alanlarını bulabilirsiniz:

1. Programlama: Armstrong sayıları, programlamada özellikle döngüler ve dizi işlemleriyle ilgilenen geliştiriciler için ilgi çekicidir. Bir sayının Armstrong sayısı olup olmadığını kontrol etmek veya Armstrong sayılarını bulmak için programlar yazılabilir.
2. Sayı Teorisi: Armstrong sayıları, sayı teorisi çalışmalarında ilginç bir konudur. Bu sayıların özellikleri ve dağılımları üzerine araştırmalar yapılmıştır.

Armstrong Sayılarını Bulma Yöntemleri Armstrong sayılarını bulmak için farklı yöntemler kullanılabilir. İşte iki yaygın yöntem:

1. Basit Döngü Yöntemi:
   • Sayı aralığı belirlenir.
   • Her bir sayı için rakamların küplerinin toplamı hesaplanır.
   • Hesaplanan değer, orijinal sayıya eşitse, bu bir Armstrong sayısıdır.
2. Dizi Yöntemi:
   • Sayı, dizi olarak ayrılır.
   • Dizi üzerinde döngü kullanılarak her bir elemanın küpü alınır.
   • Küplerin toplamı, orijinal sayıya eşitse, bu bir Armstrong sayısıdır.

Python ile Armstrong Sayılarını Bulma

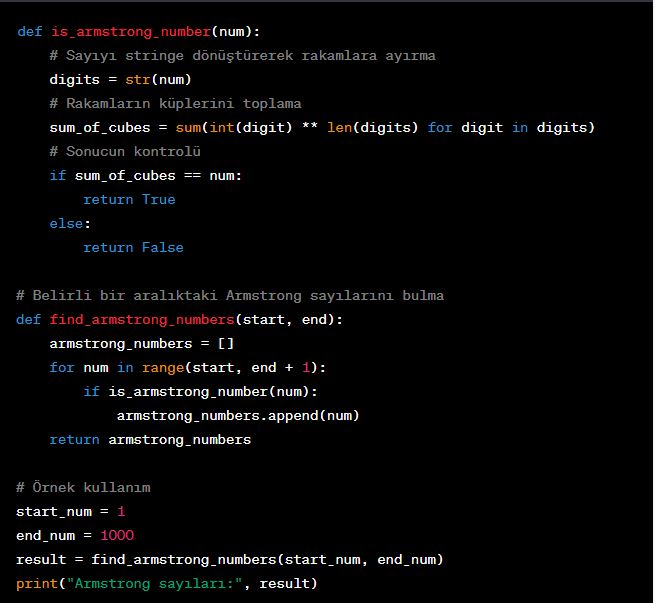
1. is_armstrong_number(num) fonksiyonu, bir sayının Armstrong sayısı olup olmadığını kontrol eder. Bu fonksiyon, num adında bir parametre alır.
2. Fonksiyonun içinde, sayıyı stringe dönüştürerek rakamlara ayırıyoruz: digits = str(num). Bu işlem sayesinde, sayıdaki her bir rakama ayrılmış bir liste elde ederiz.
3. sum_of_cubes adında bir değişken oluşturarak, rakamların küplerinin toplamını hesaplıyoruz. Bunun için, dizi üzerinde döngü kullanarak her bir elemanın küpünü alıyoruz ve toplamı hesaplıyoruz: sum_of_cubes = sum(int(digit) ** len(digits) for digit in digits). Burada, int(digit) ile her bir rakamı tamsayıya dönüştürüyoruz ve ** operatörüyle küpünü alıyoruz. Toplama işlemi sum() fonksiyonuyla gerçekleştirilir.
4. Son olarak, hesapladığımız sum_of_cubes değerini orijinal sayıyla karşılaştırarak, sayının Armstrong sayısı olup olmadığını kontrol ediyoruz. Eğer iki değer birbirine eşitse, True değerini döndürüyoruz. Aksi takdirde, False değerini döndürüyoruz.
5. find_armstrong_numbers(start, end) fonksiyonu, belirli bir aralıktaki Armstrong sayılarını bulmak için kullanılır. start ve end parametreleri, aralığın başlangıç ve bitiş değerlerini temsil eder.
6. Fonksiyonun içinde, armstrong_numbers adında boş bir liste oluşturuyoruz.
7. Ardından, range(start, end + 1) ifadesiyle belirtilen aralıktaki her bir sayı için döngü oluşturuyoruz.
8. Döngünün içinde, is_armstrong_number(num) fonksiyonunu kullanarak her bir sayının Armstrong sayısı olup olmadığını kontrol ediyoruz. Eğer Armstrong sayısı ise, bu sayıyı armstrong_numbers listesine ekliyoruz.
9. Döngü tamamlandığında, armstrong_numbers listesini döndürüyoruz.
10. Son olarak, örnek bir kullanım için start_num ve end_num değişkenlerine başlangıç ve bitiş değerlerini atayarak find_armstrong_numbers(start_num, end_num) fonksiyonunu çağırıyoruz. Bulunan Armstrong sayılarını result değişkenine atıyoruz.
11. En son olarak, bulunan Armstrong sayılarını ekrana yazdırıyoruz: print("Armstrong sayıları:", result).

Bu şekilde, is_armstrong_number() fonksiyonu ile bir sayının Armstrong sayısı olup olmadığını kontrol edebilir ve find_armstrong_numbers() fonksiyonu ile belirli bir aralıktaki Armstrong sayılarını bulabilirsiniz.

Scratch ile Armstrong Sayılarını Bulma

Scratch, görsel bir programlama dilidir ve bu dilde de Armstrong sayılarını bulmak mümkündür. İşte basit bir Scratch programı örneği:

1. Scratch’te, bir “dizi oluştur” bloğu kullanarak “Armstrong Sayılar” adında bir dizi oluşturun ve başlangıç değerini ayarlayın.
2. “Armstrong Sayılar” elemanlarını artırmak için bir döngü bloğu kullanın.
3. Döngünün içinde, değerin basamaklarındaki sayıları bulan “x. harfi” kodunu kullanın.
4. Ayırdığınız rakamları küplerini almak için bir döngü bloğu kullanın ve toplamını hesaplamak için bir “toplama işlemi” bloğu kullanın. Eğer eşit ise değeri listeye ekleyin.
5. Toplamı, orijinal sayıyla karşılaştırarak Armstrong sayısını kontrol edin ve sonucu göstermek için bir “mesaj göster” bloğu kullanın.
6. Döngüyü sonlandırmak için bir “tekrarla” bloğu kullanın.

Bu Scratch programı, tespit ettiği sayıları eleman olarak Armstrong dizisine ekleyecektir. Programı çalıştırdığınızda, Armstrong sayılarını gösteren bir mesaj alacaksınız.

Sonuç Bu makalede, Armstrong sayılarının ne olduğunu, tarihçesini, kullanım alanlarını ve bulma yöntemlerini ele aldık. Python dilinde Armstrong sayılarını bulmak için örnek bir kod ve Scratch ile Armstrong sayılarını bulmak için basit bir program örneği sunduk. Armstrong sayıları, matematiksel ilgi alanlarından programlama uygulamalarına kadar birçok alanda önemli bir rol oynayabilir.